Getting Started with Amazon S3

Read More

Predicting the onset of Diabetes - II

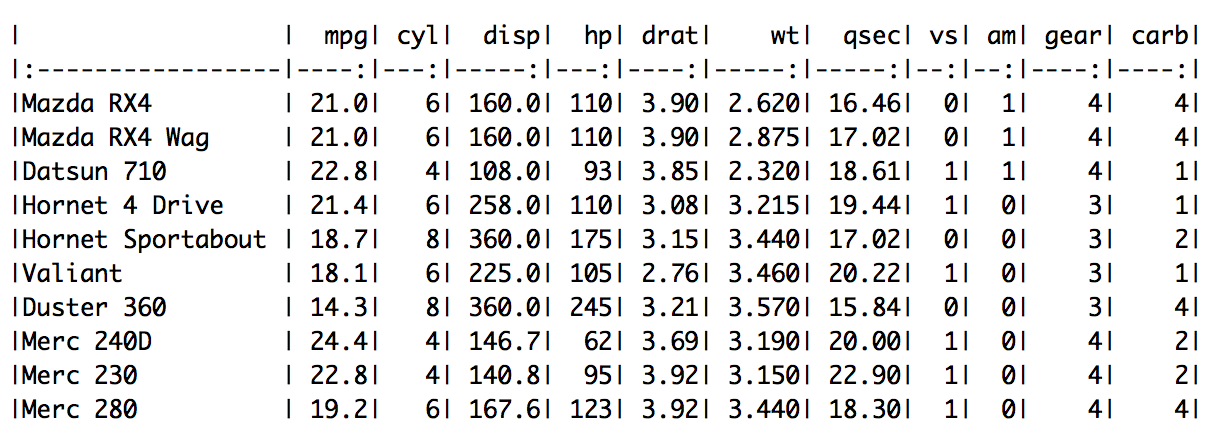
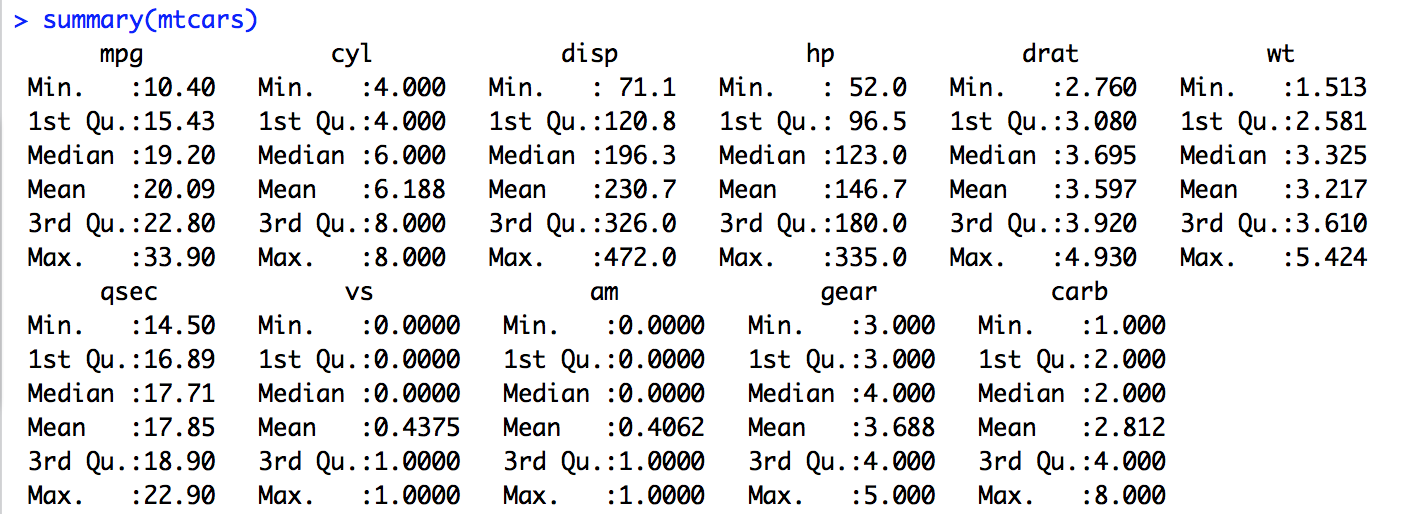
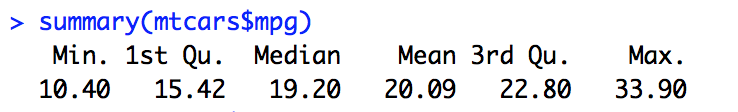We concluded our previous attempt to predict the onset of diabetes with a few questions. Lets try to answer the questions in this post.

Recap

The model that we built previously had an accuracy of 77.73% - with a caveat that we used the same data for training the model and do the prediction. And we had a few questions.

Is there a better model to predict? If so, how do we build and measure it?

Yes. There can be many models that we can build on the data set. Lets try to build one more and try to measure it.

Are there any disadvantages in building the model and testing the model on the same data set?

Certainly, its like looking at the questions that ll be asked before taking an examination. Any average person can memorize the answers and can increase the chance of scoring better marks in the exam. Same is the case with the model that we build. It stands a better chance and accuracy if we work on the same data set to predict.

A different model - Decision Trees

Lets try to build a decision tree (without going through the math behind them) on the data set . We ll use the model to make prediction (as we did earlier). We ll also measure the accuracy of the model.

Here we ll build a Decision Tree using Recursive Partitioning to classify the data. The technique is to classify members of the population by splitting it into sub-populations based on several dichotomous independent variables. The process is termed recursive because each sub-population may in turn be split an indefinite number of times until the splitting process terminates after a particular stopping criterion is reached.

A major advantage with this method is this is very simple and more intuitive.

rpart.fit <- rpart(Outcome ~ .,data=pimaimpute)
prp(rpart.fit, faclen = 0, box.palette = "auto", branch.type = 5, cex = 1)

Doing that produces this beautiful Decision Tree.

How to read this?

The model splits the data set into two sections based on Glucose Level and then on Age (for the section where Glucose level is <128) and on BMI and so on until it finds stopping criteria.

As we have build the model, lets use this model for predict (on the same data set).

rpart.pred <- predict(rpart.fit, data=pimaimpute, type = "class")


Lets predict the accuracy of this model.

Confusion Matrix Visualized

Closing Notes

This model has got an accuracy of 83.98% (versus our Linear Model's accuracy of 77.73%).

One important question that we ll address in the next post is - 

Are there any disadvantages in building the model and testing the model on the same data set?

P.S.: The complete code that was used for this article is here.

Read More

Predicting the onset of Diabetes

One of the applications of Machine Learning is to predict likelihood of occurrence of an event from the past data. With our learning from exploring data to testing hypothesis, lets see if we can put together the learning to predict likelihood of onset of diabetes from diagnostic measures.

Data Source

We would be working on Pima Indians Diabetes Data Set from UCI Machine Learning Repository.

Data Set Information

This data set is originally from the National Institute of Diabetes and Digestive and Kidney Diseases. This data set contains diagnostic measures for female patients of at least 21 years of age who belong to Pima Indian Heritage.

Please note: This is a labelled data set.

Number of Records                  :        768
Number of Attributes               :            8

Attribute Information

1. Number of times pregnant 
2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test 
3. Diastolic blood pressure (mm Hg) 
4. Triceps skin fold thickness (mm) 
5. 2-Hour serum insulin (mu U/ml) 
6. Body mass index (weight in kg/(height in m)^2) 
7. Diabetes pedigree function 
8. Age (years) 
9. Class variable (0 or 1)

Taking a quick glance at the data

Please note: The column names are shortened for convenience

The action begins

Now we have sourced the data, using our learning lets start exploring the data.

Summarizing the data set is a simple but powerful step to start understanding the data. As we can see here, there are a few measures with zero values which are biologically impossible (example would be blood pressure). Now this leads us to the next action of handling the missing/invalid data. And its also a good idea to visualize the data.

A Quick Look

As the visuals suggest, Glucose, Blood Pressure, Skin Thickness, Body Mass Index are normally distributed while are Pregnancies, Insulin, DBF, Age exponentially distributed.

Also please have in mind that this visuals are rendered without handling for the missing values. The next step is to handle or treat the data for missing values.

Data Preparation

Missing Values

There are zero value entries for the following measures. We ll impute them with mean value for corresponding measure.

• Glucose
• Blood Pressure
• Skin Thickness
• Insulin
• Body Mass Index

Pregnancies

Quick tabulation on this column shows that minimum value being zero (permissible) and maximum value being 17 (still theoretically possible even though this is an outlier).

Just to cross-check the feasibility lets look at the record and check the Age (which is 47). This suggests that this can be possible (at least theoretically).

As the values of Pregnancies seem to be biologically valid, no data handling is needed.

Visualizing Missing Values

Before Imputing

After Imputing

With cleaner data, we are geared up for building models and do the prediction.

Building a model

We try to build a logistic regression model on the data as the Outcome is categorical.

This is easy, isn't it?

The summary gives us interesting information (listed below).

Out of eight features that we have, four stand out to be significant on influencing the person to be diabetic or not (Outcome)

• Pregnancies
• Glucose
• BMI
• DPF 

Lets looks at the Odds Ratio to see to what extent these features are influencing the Outcome.

Odds Ratio

Each pregnancy is associated with an odds increase of 13.31%
Each unit increase of plasma glucose concentration is associated with an odds increase of 3.80%
An unit increase in BMI increases the odds by 9.76%
For every unit increment in DPF, the odds are up by 137.76%

Prediction

Here comes the interesting part. Having built a model that can predict the likelihood of onset of diabetes, lets try to do some prediction and see how well does this model work.

Here is the confusion matrix from prediction.

Confusion Matrix Visualized

Closing Notes

This model has got an accuracy of 77.73% but the point to be noted here is the model used the same data to do the prediction.

Now a few questions that linger our mind are
Are there any disadvantages in building the model and testing the model on the same data set?
How can we apply this model in a new data with confidence?
How can I ensure this is a good model to predict?
Can I build a better model?
and so on.

Lets try to answer these questions (and more) in the subsequent posts.

P.S.: The complete code that was used for this article is here.

Read More

mtcars - Hypothesis Testing

Having explored the mtcars dataset and building a good understanding about the dataset, its time for us to do some "Hypothesis Testing" (without getting much into math and statistics behind it).

Hypothesis Testing

So, the objective of this testing is to state our hypothesis about cars and validate our conclusion that the result was not by chance and it can be explained by data. If we are able to do that, we would prove our hypothesis to be true. Otherwise we ll reject our hypothesis.

Lets define the steps of the hypothesis testing (as below)

• Define the hypothesis
• Collect the data (this is already done)
• Use the data and statistic measures to bolster/bust the hypothesis 

Hypothesis Definition

Let us frame our hypothesis like -  Cars fitted with manual transmission have high fuel efficiency when compared with cars with automatic transmission.

null hypothesis -> True difference in fuel efficiency means between two groups of cars is = 0

alternate hypothesis -> True difference in fuel efficiency means between the groups is not = 0

Testing the Hypothesis

On trying to get average mpg across the two classes of transmission type, we see cars with manual transmission runs ~7.25 more miles per gallon when compared with their peers fitted with automatic transmission.

Here is the visual of the fuel efficiencies by transmission type.

t.test() result summary from R looks like this.

Since the p-value is 0.001374 (which is less than 0.05) we can reject the null hypothesis. But before doing so, lets try to quickly quantify by building a simple linear regression model and see if the model explains the variability.

Simple Linear Regression

Looking at the coefficients from the result summary we get the same information (of cars with manual transmission having ~7.25 mpg more). Interestingly, the R-Squared value explains that only 36% of variability in data is explained by the model - we should dig a little deeper to understand what other feature(s) can explain the variability.

What can we do next?

From the correlation tests, we understood that mpg is (negatively) correlating with wt, hp and disp (in addition to am).

A better idea is to build a multiple linear regression model including explanatory variables wt, hp and disp and see if the data variability can be explained.

Multiple Linear Regression

A few observations:

1. 84% of the variability in the data can be explained by this multiple linear regression model and hence we reject our null hypothesis
2. Interestingly, the fuel efficiency difference between cars with manual and automatic transmission is about ~2.15 miles per gallon
3. The feature that influences fuel efficiency the most is the Horse Power followed by weight of the vehicle and the transmission type is an insignificant influencer

Image from LiveJournal found via xkcd

Conclusion

From data, we were able to conclude that though manual transmission cars have higher fuel efficiency that cars fitted with automatic transmission, the transmission type has no significant impact on the fuel efficiency of the car (with the best model that explains the variability in data) and also in the journey we were able to find the factors that impact the fuel efficiency.

P.S.: It is wise to note that the dataset we have used is at least four decades old and with technological  improvements in automobile industry our study might not be relevant. Nevertheless, we have tried building a model that can be applied to similar datasets that are from today.

Read More

Lets Explore Data - II

In the previous post we understood the "mtcars" data set and did some univariate analysis to understand the features from the data set.

The objective of this post is to understand how multiple features (aka variables) are related. For example, one might be interested in understanding how weight of the car affects its fuel efficiency.

Correlating Weight of the Car to its Fuel Efficiency

Here is the visual representation of the relationship between weight of the car to its fuel efficiency (mpg).

From this plot, its evident that weight and mpg are inversely related which means lower the weight of the car more the miles per gallon is (i.e. more is the fuel efficiency of the car).

Testing Statistically

To statistically validate this relation and to ensure that this is not by chance, we ll perform correlation test. This can be achieved by cor.test() command in R.

Couple of things to look at the results from Correlation Test is p-value and correlation coefficient.

The smaller the p-value, the more significant the correlation, so here we can be very confident that a correlation exists.

Correlation Coefficient is a number between +1 and −1 calculated so as to represent the linear interdependence of two variables. +1 represents a perfectly linear positive relationship while -1 represents a perfectly linear negative relationship. 0 indicates that the two variables are not correlated.

Inference 

p-value from the above correlation test is a extremely small number which suggests a strong correlation exists.

Correlation Coefficient being -0.87 suggests that the relationship between these two variables are negative (i.e. they are inversely related).

Both the p-value and for suggest that the variation that is observed in the data set is not by chance and there is a interdependence between the variables.

This is a powerful way for understanding correlation between two variables. Now, can we extend this to all the numeric variables in mtcars data set and does it still make sense?

Lets see.

Extension

Well, this chart gives us the relationship between multiple variables but its has a few problems such as it is cluttered and also its redundant (the plots are mirrored across the diagonal).

Lets make it pretty by tweaking this plot a little bit.

This looks much clearer and also gives us the correlation coefficient in the upper half of the plot with text size proportional to the value to improve readability.

We observe stronger negative correlation between the following variable pairs

• mpg & wt
• mpg & disp
• mpg & hp
• drat & disp

and stronger positive correlation between the following variable pairs

• disp & wt
• disp & hp

A Better Visualization? May be!

This visualization gives a sense of which variables are in relation along with their type or relationship (as indicated by the color/correlation coefficient value). This can be an effective tool to communicate the correlation between variables. In this example, the reader can understand quickly that wt & disp are positively correlated while wt & mpg are negatively correlated.

Now a question hits our mind - if the reader is interested in building an understanding of relation between multiple variables (as opposed to just two variables) is there a way to do it?

Visualize correlation of many variables at once

Parallel Coordinate Visualization is the answer.

Parallel Coordinate is an effective visualization technique to visualizing high-dimensional geometry and analyzing multivariate data.

Note: The number of lines correspond in the plot above corresponds to number of cars in each class (highlighted by the color).

This visualization technique gives an awesome way to understand relationship between multiple variables.

With cars categorized based on number of cylinders (4-cyl cars represented by Blue lines, 6-cyl cars by Red lines and 8-cyl cars by Dark Green lines), we are able to explain the relationship between variables much quicker.

For instance - say if you follow the blue lines, its evident that mpg enjoys an inverse relationship with disp, hp & wt. This not only helps us to understand the relationship between different variables/features but also in understanding few interesting facts like cars with four cylinders are fuel efficient in general and higher horse power is obtained by eight-cylinder cars.

We are now equipped with techniques to explore and understand data.

In the next post, lets see if we can use the data to build a model to predict missing variables from similar data.

Read More

Lets Explore Data - I(a)

I thought it would be a good idea to visually explain the inferences from the previous post because a picture is worth a thousand words. Visualization is one of the most effective ways to communicate the findings from Data Analytics.

This post would be a shorter one as we are going to visually represent the analysis we did in the previous post.

I am using R to explore the data. Please feel free to use tool of your choice for data exploration.

Descriptive Statistics on "mpg"

Summary Statistics - Miles Per Gallon

The above "box plot" would give the five number statistics (minimum, lower quartile, median, upper quartile, maximum) and Mean.

Distribution of cars based on number of cylinders

Distribution of cars based on number of forward gears

Distribution of cars based on transmission and on engine type

We can also combine different aspects/parameters and chart them together

In the next post, we ll see about multivariate data analysis.

Read More

Lets Explore Data - I

Having acquainted with The ABCs of Machine Learning, its time to do some data exploration to understand the nature of data to graduate to the next level.

After we acquire data, the immediate next step would be to make sense of the data, quickly. This step would be of paramount importance as doing this right would help in saving lots of time while we build model/draw conclusion.

Data Set

The data that we are going to explore is sourced from here.

Lets get started.

As defined, the data was extracted from the 1974 Motor Trend US magazine, and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models).

I am using R to explore the data. Please feel free to use tool of your choice for data exploration.

Quick Tip: As the data is available in csv format, Microsoft Excel would also help us in doing the data exploration.

A quick look at (part) of what is inside the data set.



Here is the metadata for the data set.

Variable Name	Description	Variable Type
mpg	Miles/(US) gallon	Quantitative (Continuous)
cyl	Number of cylinders	Qualitative (Nominal)*
disp	Displacement (cu.in.)	Quantitative (Continuous)
hp	Gross horsepower	Quantitative (Continuous)
drat	Rear axle ratio	Quantitative (Continuous)
wt	Weight (1000 lbs)	Quantitative (Continuous)
qsec	1/4 mile time	Quantitative (Continuous)
vs	V Engine/S Engine (0=V, 1=S)	Qualitative (Nominal)
am	Transmission (0 = automatic, 1 = manual)	Qualitative (Nominal)
gear	Number of forward gears	Qualitative (Nominal)
carb	Number of carburetors	Qualitative (Nominal)

* Depending on the analysis that we do using "cyl" this can be classified as Quantitative (Discrete) too.

I have also mapped the variable name and description with the variable type. Please have a quick look to review the same. If there are any questions, please ask them in the comments section.

After we skim through the metadata and understand the variable properties, next step is to get descriptive statistics on the data set. Descriptive Statistics include frequencies (counts), ranks, measures of central tendency (e.g., mean, median and mode), and measures of variability (e.g., range and standard deviation). These help in developing good and quick understanding of the data.

Remember we would want to do numeric operations only on the Quantitative Variables even though some of the Qualitative Variables that have numeric values (e.g., vs, am, etc)

Descriptive Statistics on "mpg"

Average Miles Per Gallon

Median Miles Per Gallon

Miles Per Gallon Range

Summary Statistics - this captures all of that we calculated earlier at one shot

Inference on mpg

The mpg (for all the vehicles in the data set) ranges from 10.40 miles per gallon to 33.90 miles per gallon with an average of 20.09 miles per gallon and median 19.20 miles per gallon.

Please note: summary() in R gives another interesting measure "IQR" (interquartile range) which we ll read about in a future post.

Extending the Descriptive Statistics to the other variables of interest (mpg, weight, gear, am, vs, cyl) in the data set yields us the following.

Inference on mtcars data set

• Total number of cars in the data set - 32
• Distribution of cars based on number of cylinders is as below

  Number of Cylinders	Number of Cars
  Four	11
  Six	7
  Eight	14

  
  
• Distribution of cars based on number of forward gears is as below

  Number of Forward Gears	Number of Cars
  Three	15
  Four	12
  Five	5

  
  
• Distribution of cars based on transmission is as below

  Transmission Type	Number of Cars
  Automatic	19
  Manual	13

  
  
• Distribution of cars based on engine type is as below

  Engine Type	Number of Cars
  V-Engine	18
  Straight Engine	14

  
  
• Miles Per Gallon ranges between 10.40 mpg to 33.90 mpg
• Weight of the cars range between 1513 lbs to 5424 lbs

Conclusion

We did univariate analysis on the variables in the "mtcars" data set to understand more about the content of the data set. Descriptive Statistics helps us get a good understanding about the data, quickly. We also reinforced our learning about the variable types and we are able to apply different operations for different variable type (e.g., we did not do an average on a Qualitative Variable).

We would continue to do more analysis (involving multiple variables) to make more sense on these data set in the next post.

Gist

A short hand way in R to get descriptive statistics of a data set.


Summary Statistics on "mtcars" data set


Use summary() command with caution as it treats all the variables that appear to be number as Quantitative irrespective of whether they are Quantitative or not.

Based on the type of the variable, summary() function gives different output.

• Gives the range, quartiles, median, and mean & number of missing values (if any) for Quantitative Variables
• Gives a table with frequencies & number of missing values (if any) for Categorical Variables

How to handle Qualitative Variables

The results of the summary() has given Quantitative statistics on Qualitative data - how to handle this?

Change the type of the variable (as a categorical) on the fly and we can compute frequency on the Qualitative variable.

 




Please Note: The above is an example of changing the type of one variable from the data set. We can also do this treatment as we do preprocessing before we do the descriptive statistics on the data set.

---

Note #1 : Based on the feedback (in the comments section), I would plan to write a post detailing on these measures (such as mean, range, etc) and explain the significance and on which variable types/when/where these should be used.

Note #2 : I also think of a post on "getting started with R" - if there are takers. Please leave comments if you are interested.

Note #3: Visualizing the data would be another powerful and significant method in exploring data. Please watch out for a post on the same.

Read More